This is the first in a series of posts that we intend to do about the incredible work being done at Pathfndr to create the world\’s only AI-powered Travel Operating System for travel advisors.
Ever felt annoyed while booking a flight ticket online due to the thousands of options available? The answer is probably yes. And this annoyance increases multifold when you have to do the same for international travel.
If you are spending more than 60 seconds looking for the perfect flight, you are spending too much time.Tweet
Decision-making is a mental and cognitive process, and with the vast development of e-shops, users are forced to do this more and more. For a mundane task like booking a flight ticket, one should not have to go through this level of mental strain. Such decision-making is not even rewarding because you are never fully sure whether you optimized for all the underlying evaluation criteria. Of course, this assumes that a reasonably rational person is looking to book the flight and agrees that:
- The cheapest flight may be the best flight, but is not necessarily so
- The shortest flight may be the best flight, but is not necessarily so
- The best airline does not always operate the best flight between sectors
and so on…
Pathfndr is a one-stop solution for all travel decision-making, with many verticals such as Where to go? How to get there? Where to stay? What to do there? … including Intelligent Dynamic Packaging doing all of the above.
Such decision-making depends on several tangible and intangible factors, which can appear to be chosen arbitrarily by the decision-makers. At Pathfndr, we aim to demystify the science behind those seemingly arbitrary decisions by decluttering the thinking process and translating that into clear and objective mathematical criteria.
THE PROBLEM
Choosing a flight depends on a number of factors, such as flight price, trip duration, the motive of the trip, departure time of the flight etc. Our goal is to provide the customer with a list of flights ranked in order of relevance considering the highest possible number of factors including both the customer’s intent at that point in time and the flights’ availability and pricing data for that origin-destination pair at the time of search.
OUR SOLUTION
Now a very obvious choice of solution for such problems seems to be a \’learning to rank\’ algorithm. However, all the approaches associated with LETOR require training algorithms on ordered data or partially ordered data at the least. Also, LETOR approaches can be very sensitive to noise in the data. When a ranking function is learned from clickstream data on a previous, non-optimized ranking, the observed preferences can contain biased information. Items that appeared at the top of the non-optimized ranking may have enjoyed customers’ interest without being truly preferred.
Seeing all these challenges, to create our proprietary flight ranking algorithm, we improvised on a classic approach to help decision-makers known as Analytical Hierarchy Process (AHP). This process, originally proposed by Thomas L. Saaty is a very popular approach to multi-criteria decision-making that involves qualitative data. It provides a way of breaking down the decision-making into a hierarchy of sub-problems, which are easier to evaluate. There is a lot of literature1,2 available by Saaty himself explaining the origin and development of the Analytical Hierarchy Process over the years.
At a high level,
AHP works as a decision-maker, i.e., Deciding amongst various alternatives available by assigning scores to all such alternatives by taking into account all the factors affecting this decision process. AHP considers a set of evaluation criteria and a set of alternative options among which the best decision is to be made. It is important to note that, since some of the criteria could be contrasting, it is not true in general that the best option is the one that maximizes every single criterion, rather it\’s the one that achieves the most suitable trade-offs among the different criteria.
It generates a weight for each evaluation criterion according to the decision maker’s pairwise comparisons of the criteria. Next, for a fixed criterion, the AHP assigns a score to each option according to the decision maker’s pairwise comparisons of the options based on that criterion. The higher the score, the better the performance of the option with respect to the considered criterion. Finally, the AHP combines the criteria weights and the options scores, thus determining a global score for each option, and a consequent ranking. The global score for a given option is a weighted sum of the scores it obtained with respect to all the criteria.
The idea is to
- Assign weights to the evaluation criteria for the variety of users
- Assign weights to all the alternatives for one criterion at a time and create a matrix for option scores
- Calculate overall score by using above matrices and rank the alternatives
#1 - Assign weights to the evaluation criteria for the variety of users
Based on the traveler type as well as travel intent, we segment our users into different categories such as budget-sensitive users, duration-sensitive users, family users, short-haul, etc depending on the possible search parameters. And we create a criteria weight vector for each user category
A snapshot of the evaluation criteria considered is as follows
- Price
- Outbound Departure Time
- Outbound Arrival Time
- Inbound Departure Time (Two way flight case)
- Inbound Arrival Time (Two way flight case)
- Outbound number of stops
- Inbound number of stops (Two way flight case)
- Outbound total layover/duration
- Inbound total layover/duration (Two way flight case)
There are several other features which we use and more that we plan to include at a later point in time as this information gets more organized/ we organize it.
We create a positive reciprocal matrix A from the pairwise comparison of the evaluation criteria i.e. an mxm matrix if there are m evaluation criteria.
Each entry ajk of the matrix A represents the importance of the jth criterion relative to the kth criterion. If ajk > 1, then the jth criterion is less important than the kth criterion while if ajk < 1, then the jth criterion is more important than the kth criterion. If two criteria have the same importance, then the entry ajk is 1.
The entries ajk and akj satisfy the following constraint:
ajk . akj = 1
Hence, ajj = 1 for all j.
A sample criteria pairwise comparison positive reciprocal matrix look like this
| Criteria | c1 | c2 | c3 | c4 | c5 |
| c1 | 1 | 1/3 | 1/3 | 1 | 1/5 |
| c2 | 3 | 1 | 1 | 3 | 2 |
| c3 | 3 | 1 | 1 | 3 | 2 |
| c4 | 1 | 1/3 | 1/3 | 1 | 1/2 |
| c5 | 5 | 1/2 | 1/2 | 2 | 1 |
This matrix usually comes out to be a small perturbation of a consistent matrix, as it reflects our cardinal inconsistency of estimating precise measurement values even from a known scale and worse when we deal with intangibles i.e. a is preferred to b twice, b is preferred to c thrice, but a is preferred to c only four times and ordinal intransitivity (a is preferred to b, b is preferred to c but c is preferred to a). One reason for filling out the entire matrix is to improve the validity of judgments.
From this matrix, we want to derive the priorities of all the criteria in the form of a weight vector. Now a priority vector derived from an arbitrary positive reciprocal matrix has much less validity than a consistent one or a near consistent one. The aim is to make this matrix close to a consistent matrix using additional information but without forcing it. Forcing a consistent matrix without knowing precise values is arbitrary and the derived priority loses all validity in making an underlying decision. Moreover, doing this in practice would require people to act in a robotic manner, lose their ability to change their minds on new evidence, and be unable to make judgments representing their feelings. There are ways to check the consistency of a matrix as suggested by Prof. Saaty himself. Another paper discusses and challenges some of the widely accepted ways of accepting or rejecting a pairwise comparison matrix.
In this paper, it has been shown that with dominance order, the principal eigenvector, known to be unique to within a positive multiplicative constant (thus defining a ratio scale), and made unique through normalization, is the only plausible candidate for representing priorities derived from a positive reciprocal near consistent pairwise comparison matrix.
w = normalised(Eig(A)) << Priority vector/weight vector
#2 - Assign weights to all the alternatives for one criterion at a time and create a matrix for option scores
The matrix of option scores is a n×m real matrix S; where n is the number of alternatives and m is the number of criteria. Each entry sij of S represents the score of the ith option with respect to the jth criterion. In order to derive such scores, a pairwise comparison matrix Bj is first built for each of the m criteria, j=1,…,m. The matrix Bj is a n×n real matrix. Each entry bihj of the matrix Bj represents the evaluation of the ith option compared to the hth option with respect to the jth criterion.
These matrices are created using the live flight alternatives available at the time of user search, and assigning numerical estimates as stated above remains challenging. For example, let\’s say you have to compare two flight options for departure time, one departing at 10 AM and one at 4 AM. Now suppose that in order to prioritize for convenience, we might want to suggest that the former is a better choice, but how do we quantify this preference. This is where we had to come up with defining the utility of timings (arrival/departure for inbound, outbound). We have analyzed historical flight data and used monte-Carlo simulations to approximate the utility for departure/arrival timings. Further customization was done to correct the different segments of users by shifting or shrinking utility curves. Other criteria such as layover and price are handled by doing dynamic bucketing.
After all this, there is still one challenge left to be resolved, that it requires us to do a pairwise comparison of all the criteria and all the alternatives for each criterion. Now the number of criteria is usually limited but the alternatives are fed into the model at run time and the number tends to be in the range of thousands. Let\’s observe the number of computations in AHP
Let’s say there are n alternatives and m criteria
| n | m | #computations |
| 10 | 5 | 235 |
| 50 | 5 | 6135 |
| 100 | 5 | 24760 |
| 500 | 5 | 623760 |
| 1000 | 5 | 2497510 |
This is an exponential increase in the # computations which further increases the processing and the latency when the total flights to be ranked are increased.
To handle this, we take the unique set of alternatives for each criterion, create a pairwise comparison reciprocal matrix for those alternatives, calculate a weight vector for the unique alternatives, do a lookup/map to fill the priority of all the remaining duplicate alternatives for that criteria and normalize to get a final weight vector. Hence matrix Bj is a kj × kj real matrix, where kj is the number of unique options evaluated for criteria j. Therefore instead of performing nC2 computations in Bj, we are doing kjC2 computations.
#3 - Calculate overall score by using above matrices and rank the alternatives
Multiply the option score matrix and weight matrix from the above two steps
i.e v = S*w
The ith entry vi of v represents the global score assigned by the AHP to the ith option. As the final step, the option ranking is accomplished by ordering the global scores in decreasing order.
Experimentation
We developed an offline tool to test flight rankings on limited flight options covering the edge cases observed and outlined by the team. This model worked fine when it was run as an offline prototype. It was later deployed for an online experiment where it did not perform well initially. This was not a big surprise though. Just because a model has performed well on past data, it need not perform as well on unseen/future data. The failed cases were studied offline thoroughly. Apart from the unseen flight data issue, poor-performing cases included searches with a very high trip budget, a group of travelers from different age groups, origin, and destination in different time zones, etc. It helped us eventually figure out both new segments of users and missing/duplicate features for different types of searches. We also ended up creating a feedback pipeline which helped us further refine the utility curves and optimize the dynamic bucketing algorithms for features.
A little more
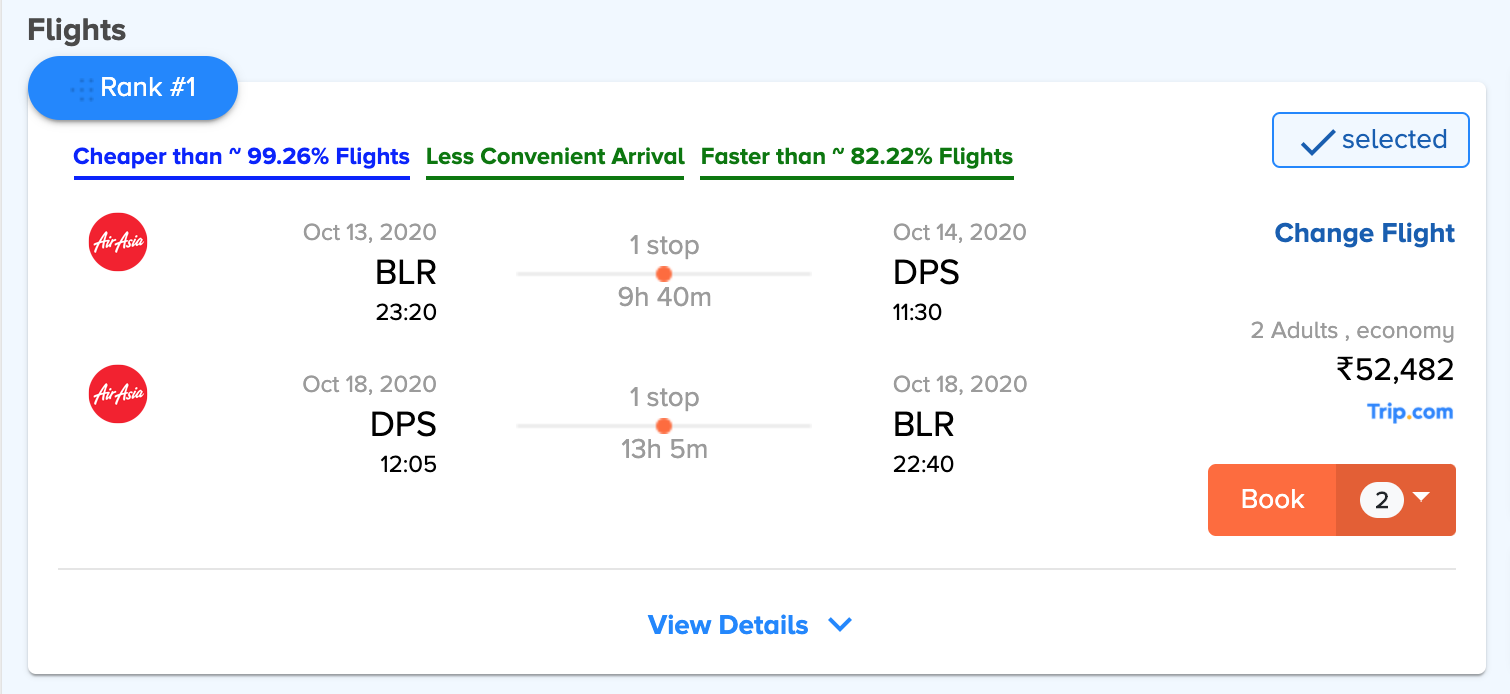
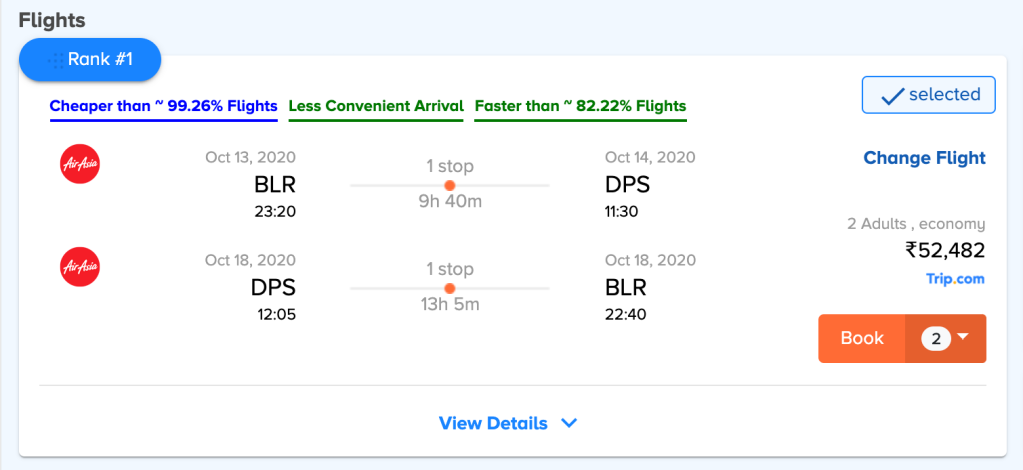
No matter how well you have understood the user requirements and optimized the rankings accordingly, the job is not done until you have communicated the same to the user. Many times, even after making a choice, user satisfaction is hindered by the uncertainty of the choice being a good one. Therefore, for further validation of the rankings for users, to answer the \”why\” of making the choice, we provide relevant stats for the shown flight itineraries.
Future work
This ranking approach however has managed to achieve good results so far, it is still an ongoing development. Using this approach, we hope to gather enough flight booking data on optimized ranking, which can further be verified or modified into a self-learning model.
P.S.
- If you are academically interested in learning more, or a consumer who has feedback to share, write to us at [email protected].
- If you are a travel company that wants to license our flight ranking technology, write to us at [email protected]. Go to www.pathfndr.io to see more about our technology licensing business.
References
- T.L. Saaty, The Analytic Hierarchy Process. ( New York 1980).
- T.L. Saaty, Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process. RWS Publications Pittsburgh 1994).
- T.L. Saaty, Decision-making with the AHP: Why is the principal eigenvector necessary. University of Pittsburgh, Pittsburgh, PA 15260, USA.